Analyze Existing Subnet Masks 4
This post asks you to analyze the choice of subnet mask in a network. If a company uses one subnet mask for all subnets of one classful network, you can analyze the address structure as three parts: Network, Subnet, and Host. Then, you can calculate the number of subnets possible with these design choices. You can also determine the size of each subnet.
For those who care to pass Cisco certifications, you should strive to get the answer to each problem in about 15 seconds. This post gives you five problems. Get a stopwatch or clock app open and get ready to practice!
Videos: How to and More Practice
The left video discusses the design approach to subnet masks, which begins with the choice to use only one subnet mask within the entire classful network. Then, you consider the number of subnets the design requires, plus the size needed for each subnet, to determine which masks will work—and then choose among those masks.
The right video provides some practice with the process.
Five Practice Problems (Hidden)
You may make the following assumptions:
- All subnets of the network use the same mask (as listed with the problem).
- All subnets can be used, including the zero subnet and broadcast subnet.
Each problem supplies a classful network (a class A, B, or C network) and the mask used by all subnets. Your job:
- Analyze the address structure to determine the number of Network, Subnet, and Host bits.
- Calculate the number of subnets in the design.
- Calculate the size of each subnet.
For any values that use a power of 2 above 2^16, you may leave your answer in exponential form.
| Problem | Classful Network | Mask |
|---|---|---|
| 1 | 9.0.0.0 | /25 |
| 2 | 100.0.0.0 | /24 |
| 3 | 151.151.0.0 | /23 |
| 4 | 172.16.0.0 | /22 |
| 5 | 172.31.0.0 | /21 |
The following table supplies the powers of 2 and their decimal equivalents.
| 2^x | Decimal | 2^x | Decimal |
|---|---|---|---|
| 2^0 | 1 | 2^9 | 512 |
| 2^1 | 2 | 2^10 | 1024 |
| 2^2 | 4 | 2^11 | 2048 |
| 2^3 | 8 | 2^12 | 4096 |
| 2^4 | 16 | 2^13 | 8192 |
| 2^5 | 32 | 2^14 | 16,384 |
| 2^6 | 64 | 2^15 | 32,768 |
| 2^7 | 128 | 2^16 | 65,536 |
| 2^8 | 256 | 2^17 | 131,072 |
Answers and Explanations for Each Problem
First, determine the number of network, subnet, and host bits. You already know the prefix mask (/P) per each problem statement. From there:
- Determine the number of network bits per class A, B, and C rules
- Determine the number of subnet bits (S), which is the different between the prefix (P) and network bits (N): S = P – N
- Determine the number of host bits, which is 32 – P.
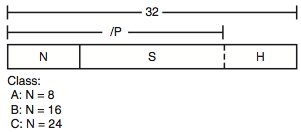
Table 1 lists the structure of addresses for each problem, while Table 2 lists the calculated number of subnets and hosts/subnet.
| Problem | Class | Network Bits (N) | Subnet Bits (S = P – N) |
Host Bits (32 – P) |
|
1 |
A |
8 |
17 |
7 |
|
2 |
A |
8 |
16 |
8 |
|
3 |
B |
16 |
7 |
9 |
|
4 |
B |
16 |
6 |
10 |
|
5 |
B |
16 |
5 |
11 |
Table 1: Network, Subnet, and Host Bits for Each Problem
|
Problem |
Number of Subnets |
Number of Hosts |
|
1 |
2^17 = 131,072 |
2^7 – 2 = 126 |
|
2 |
2^16 = 65,536 |
2^8 – 2 = 254 |
|
3 |
2^7 = 128 |
2^9 – 2 = 510 |
|
4 |
2^6 = 64 |
2^10 – 2 = 1022 |
|
5 |
2^5 = 32 |
2^11 – 2 = 2046 |

Hello Wendell,
First off, thank you for this blog and the YouTube lectures for the CCNA. I am making an attempt at teaching myself network engineering, and your content is a big help.
I noticed that the preceding three pages (including this one) are all the same problems for analyzing an existing subnet… is that correct? I’ve gone over them a few times to see if there is a difference, but I see none.
Regards,
Wow. Yep, I see what you mean. That wasn’t on purpose. So, I’ll get those fixed! So sorry about that. I’m travelling, so I won’t get it fixed this week, but I will when I return.
And you’re welcome for the content – thanks for the kind words!
I think the problem is that the click downs for the hidden problems on all 4 pages point to the same link: #1721854165325-62065523-1afe
Hope this helps, I really appreciate these practice problems! They’ve helped me finally understand a concept I’ve struggled with for years.