STP Puzzle #2 – Answer
If you didn’t see the puzzle problem statement, then the answers won’t make as much sense. Especially for this one, the new post this week that gives some suggestions on how to attack these STP puzzles can help. The realization that on a switch-to-switch link, the two ends are either a designated port/root port combi, or a designated port/blocking port combo, really streamlines thinking through the STP topology. Answers below the fold. Enjoy!
Step 1: Rule Out Switches from Being Root Switch
In the post where I suggest how to attack these problems, I suggest starting by finding the root switch. Everything in the STP topology revolves around the root, so that makes sense. In this puzzle, you can directly rule out S3 and S4, as follows:
- The problem statement says that S4’s BID is worse (higher) than S3’s BID, so rule out S4 as root.
- S3 has a root port (RP), and only non-root switches have an RP. Rule out S3.
However, the problem does not tell us anything about S1 and S2’s BIDs, which is what STP actually uses to choose the root switch. The problem does allow us to infer which is root, but it requires a long look at the root ports (RPs) and designated ports (DPs).
Skipping Step 2 for Now: Finding All Root Ports
For you process folks out there… I tell you in the “how to attack” post that the next step should be to find each switch’s RP. However, until you know the root switch, finding each non-root switch’s RP will be almost impossible. So I’m skipping this step. FYI.
Step 3: Find All Designated Ports (DPs)
I actually picked the details of this particular puzzle to emphasize a couple of facts that most people don’t think about with STP. With the assumptions in these puzzles, STP works normally. That is, the links all work, they all trunk correctly, the trunking config does not prevent STP from working correctly, and so on. So STP will stabilize to a normal STP topology. When that happens, on every switch-to-switch link, one of two scenarios occur:
- One end is the DP, and the other is the RP
- One end is the DP, and the other is “neither”, ie neither RP nor DP
If you just take those two facts and apply them to the known topology at this point, and do not even try to be tricky or infer anything, you’d find a few more facts. Figure 2 shows the new facts in red, with the known facts (from the problem statement) in black:
Figure 2 – Directly Derived Info from the “Link Ends, Stabilized” Rules
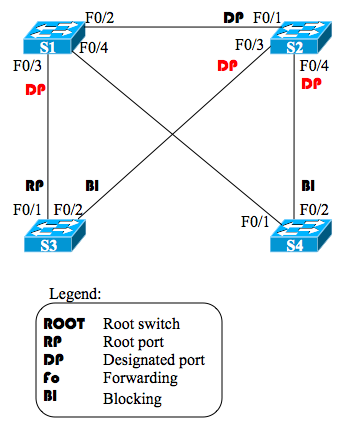
The new information (red) was found based on:
- S2’s F0/4 is a DP, because S4’s F0/2 is blocking, and is therefore neither RP nor DP.
- S2’s F0/3 is a DP, for the same reasons.
- S1’s F0/3 is a DP, because S3’s F0/1 is an RP.
With this more complete list of facts, now you can infer a lot more truth about the STP topology.
S2 is Root; It has Only DPs, and No RPs
First, from Figure 2, you can see that S2 has three DPs, but no RPs. Every non-root switch must have an RP, but the root does not have an RP at all. Therefore, S2 is the root switch.
S1’s F0/2 is its RP
Even if you did were not yet convinced that S2 was root, just based on Figure 2, S1’s F0/2 can be one of two things: an RP, which forwards, or neither an RP nor a DP, so it blocks. A link cannot have two DPs, and S2 is already a DP on the S1-S2 link.
Following this reasoning, if S1 were blocking, then there would be no STP path to/from S2, because of the combined blocking interfaces. The only choice left: S1’s F0/1 is it’s RP, making S1 not the root, and leaving on S2 to be the root.
S4’s F0/1 i its RP; S1 is the DP on the Other End
This is probably the most obvious case, but next consider S4 as shown in Figure 2. It has two ports that could be its RP: F0/1 and F0/2. However, we already know that F0/2 is blocking. So, S4’s RP must be its F0/1 port. And then S1 must be the DP on the other end of the link (S1’s F0/4).
Figure 3 shows a revised Figure 2, with the newly-inferred details in green.
Figure 3 – Final Results for DP, RP, Blocked Ports

Summary
All that logic identifies the root, all the RPs, DPs, and blocking ports. However, it does not list enough information to determine the root cost, except for S1 (RC=19). The problem also does not tell us anything about the actual Bridge ID (BID) values; in the end, S2’s BID must simply be better (numerically-smaller) than any of the other switches.

Another way to figure out the root switch without having to know the relationship of the BIDs between S3 and S4 is like this:
1. S1 F0/3 is a DP because S3 F0/1 is an RP.
2. S4 F0/1 is an RP because the switch only has two interfaces, one of which is in blocking state, and a switch must have exactly one RP unless it is the root switch. We know it is not the root switch because it F0/4 is in blocking state and a root switch has all DP ports.
3. S1 F0/4 can now be determined to be a DP port because of Step 2.
4. S1 F0/2 (the only remaining interface to be determined on S1) is either a DP or an RP depending on whether it is the root switch or not. It cannot be a DP because S2 F0/1 is a DP port, and there can only be one DP per segment. Therefore, it is an RP.
5. That leaves S2 as the only possible switch that can be the root.
Excellent explanation! Indeed, that’s another clarifying way to analyze this.
hello Wendell,
I think I am not understanding something, the following statement :
•The problem statement says that S4’s BID is worse (higher) than S3’s BID, so rule out S4 as root.
how have you derived it from the fact that the MAC address was worst, the BID is made up of the priority part and the MAC, If the priority would have been lower the BID would have been better for S3
Hi Nicola,
Working through your comment, I think:
– we agree that the problem statement claims: S4’s BID is worse than S3’s, so S4 cannot be root.
As to your last paragraph, in which you describe and ask questions, I didn’t analyze any values or break down the BID of S3 and S4. The problem begins with the fact: S4 is worst than S3. This particular post doesn’t work through the BID values, and why S4’s is worse.
I agree, if the problem here had allowed for various values, and indeed if S4’s priority was lower than S3’s, that makes S4 eligible to be root. But the problem statement doesn’t allow for that; it simply states that S4 has a worse BID than S3.
Hope this helps,
Wendell
Hello Wendell,
I believe that Nicola meant that there was some confusion at the end of the summary. For I’m sure that she meant that if the BID for S4 was “worse” than S3 as indicated by the info provided at the start of the problem, then how had you come to the conclusion, in your summary, that S4’s BID must be better (numerically-smaller) than any of the other switches? I think you meant to write “NUMERICALLY-LARGER” than any of the other switches. If I’m wrong, then please explain.
Hi Jeff,
I looked over it again, and I think you’re right – that’s what Nicola meant originally. I edited that last line of this post to refer to S2 instead of S4 as the root. Thanks much.
Wendell
I actually got this one really quickly compared to the other one. That one took me I think close to an hour, although I did mess up once and had to start over.
Yeah, these are way too complex. I’ve considered removing them and coming up with some more straightforward replacements. But a lot of folks seem to like the challenge, like getting a puzzle that you don’t want to put down. Glad this one was better for you.
Wendell
Hello Wendell,
Why did you not hightlight the use of cost to determine S1’s root port thus disqualifying it from being the root switch?
Assuming S2 as root switch
S1 F0/2 – S2 = 19
S1 F0/4 – S4 F0/2 – S2 = 19 + ?
S1 F0/3 – S3 F0/2 – S2 = 19 + ?
Clearly S1 F0/2 – S2 has the least cost hence of the 3 parts F0/2 is the RP unless you are saying it is possible for an interface cost to be 0?
Tewa,
Well, literally, if you ask me why I wrote it this way, when the pub date is 2011… I just don’t recall. 🙂
But re-reading the whole thing, I think you can guess. You can’t know whether S1 or S2 is root without a lot of analysis. Once you convince yourself S2 is the root, then your analysis makes sense. However, it’s unnecessary at that point to do the analysis you added, as all the port roles and states became obvious by the end of the analysis in the post above.
At least that’s my analysis of the above post.
Wendell